Themen

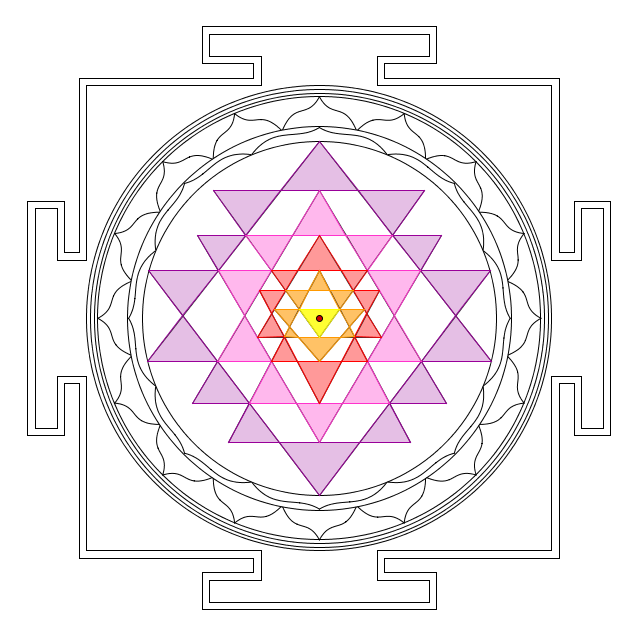
Bei meiner Reise nach Indien lernte ich einen Kulturforscher kennen, der sich schon lange mit dem Sri Yantra beschäftigt, einer Mandala-artigen, geometrischen Form, die in Indien hohe religiöse Verehrung erfährt als Meditationsobjekt. Es gilt als Sinnbild der schöpferischen Energie und des weiblichen Aspekts des Göttlichen. Dieser Forscher war auch an den mathematischen Eigenschaften interessiert und erhoffte sich von mir einige Hilfen.

Betrachtet man die innere Figur des Sri Yantra, so stellt man fest, sie ist spiegelsymmetrisch zu einer senkrechten Mittelachse und besteht aus fünf Dreiecken mit der Spitze nach unten und vier Dreiecken mit der Spitze nach oben, die in bestimmter Weise in einem Kreis mit Mittelpunkt angeordnet sind.

Will man nun diese Form einfach nachzeichnen, so wird man eine Überraschung erleben: Es gelingt nicht!

Die Figur besitzt verschiedentlich Stellen, wo sich drei Linien kreuzen. Bei meinen ersten Zeichenversuchen musste ich spätestens bei der letzten Linie feststellen, dass sie einen gewünschten Kreuzungspunkt nicht getroffen hat. 

Sehr merkwürdig!

Recherchen im Internet ergaben, dass andere Personen, die sich mit dem Sri Yantra beschäftigt hatten (z.B. Gerard Huet), vor demselben Problem standen. An einer Stelle findet sich eine schrittweise Konstruktion (von Michael Pudney), allerdings ohne Begründung. Mir scheint, es handelt sich um eine sehr gute Näherung, aber doch nur um eine Näherung.

Die in Büchern oder im Internet abgebildeten Formen weichen zum Teil ein klein wenig voneinander ab. Wegen der Strichdicke ist bei den Abbildungen nicht klar, ob sich drei Linien genau treffen oder nur angenähert. So fragte ich mich: Gibt es überhaupt ein genaues Sri Yantra oder nicht oder gar mehrere, etwas verschiedene? Ist eines davon dann das wahre Sri Yantra?

Wie wurden wohl die Sri Yantra Figuren von indischen Priestern immer wieder hergestellt? Irgendein Verfahren zur Zeichnung musste es doch geben. Nach meinen Nachforschungen in mehreren Büchern zum Sri Yantra gab es Anleitungen, die sich jedoch als fehlerhaft herausstellten. Ein Geheimnis umgab das Sri Yantra.

Angespornt durch den interessierten Forscher erwachte nun mein mathematischer Erkenntnisdrang und ich begann eine Analyse, die mit Umwegen, neuen Blickwinkeln, Fehlerkorrekturen und längeren, bis in die ersten Schultage reichenden Mühen verbunden war.

Die 9 Dreiecke sind jeweils durch die Koordinaten ihres linken Eckpunkts festgelegt, da die rechten Eckpunkte symmetrisch dazu liegen und die Spitzen in der Mitte durch den Kreis oder die Grundlinie eines anderen Dreiecks gegeben sind, d.h. wir haben 9 x- und 9 y-Koordinaten, also insgesamt 18 Unbekannte. Zählt man alle dreifachen Schnittpunkte auf der linken Seite, so kommt man auf 14 Bedingungen, die erfüllt sein müssen. So entsteht ein Gleichungssystem mit 18 Unbekannten und 14 Gleichungen. Das System ist also unterdeterminiert mit 18 – 14 = 4 Freiheitsgraden. 4 Koordinaten können also frei gewählt werden, dann hängen alle anderen davon ab. Aber wie?

Beginnt man die Konstruktion mit den beiden Eckpunkten am Kreis und den y-Koordinaten der untersten und obersten Basislinie, so kann man die Konstruktion ein Stück weit fortsetzen, d.h. manche der Unbekannten hängen recht einfach von den 4 gewählten ab. Dann kommt man zu einer Stelle, wo es nicht automatisch weitergeht.

Hier muss man ein nichtlineares Gleichungssystem mit 5 Unbekannten z.B. mit dem Einsetzverfahren lösen. Leider lässt sich die letzte entstehende Gleichung nicht einfach auflösen. Ihre Lösung ist eine Nullstelle einer gebrochen-rationalen Funktion, also muss der Zähler 0 werden, was aber immer noch ein Polynom vom Grad größer als 2 ist und wofür es keine einfache Formel gibt.

Nun hatte ich schon zu den geometrischen Konstruktionen nach anfänglichen Versuchen mit Bleistift und Papier das Mathematikprogramm geogebra  verwendet. Glücklicherweise gibt es dort einen Befehl zur (näherungsweisen) Nullstellenermittlung und mit der damit gefundenen neuen Koordinate lässt sich die Konstruktion des Sri Yantra bis zum Ende fortsetzen.

Auf diese Weise erstellte ich die geogebra-Datei Yantra-4Par (Download hier, evtl. firefox verwenden) mit 4 Schiebereglern, die es erlaubt, 4 Parameter in gewissen Intervallen frei zu wählen, so dass jedes Mal eine Sri Yantra Figur mit korrekten Schnittpunkten, aber etwas anderen Proportionen entsteht. Einer der vielen Schleier, die das Sri Yantra verhüllen, konnte also gelüftet werden.

Es bleibt die nächste Frage, ob eine dieser Formen zu bevorzugen ist, was nicht mathematisch, sondern mit außermathematischen Gesichtspunkten zu beantworten ist. Dies könnte nach dem allgemeinen ästhetischen Empfinden geschehen (ausgewogene Proportionen…), was sich möglicherweise in weiteren geometrischen Eigenschaften (z.B. 60°-Winkel, goldener Winkel…) ausdrückt. Hierzu können Sie mit Hilfe der geogebra-Datei Yantra-4Par selber spielerisch forschend tätig werden.

     

Kurven können in ausgesprochen ästhetische Formen auftreten. Die großen Möglichkeiten, die in ihrem aktiven Erfühlen liegen, werden hier angedeutet.

Eine genauere Beschreibung zu wichtigen Kurvenformen finden Sie hier.

Hier wird eine andere, ergänzende Betrachtung von Kurven dargestellt, die die Tangenten an die Kurven und damit den umgebenden Raum in den Vordergrund stellt.

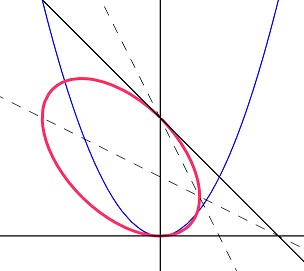
Interessanterweise bietet die projektive Geometrie eine Möglichkeit, den Bereich des Unendlichen sichtbar zu machen. Im Prinzip sehen Sie das in ähnlicher Weise auf jedem Bild, das die Horizontlinie enthält.

Eine geogebra-Datei, die Funktionsgraphen in einem projektiven Koordinatensystem ausgibt, finden Sie hier (evtl. firefox verwenden).

     

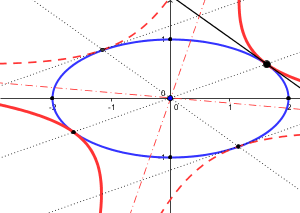
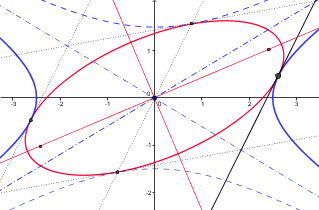
Komplexe Zahlen lassen sich auch als Pfeile darstellen. Dabei liegen die Spitzen der komplexen Punkte eines Kegelschnitts wieder auf einem Kegelschnitt. Mehr dazu finden Sie hier.

Zwei geogebra-Dateien zeigen in beweglicher Weise die Lage der Hyperbel an der Ellipse (download hier, evtl. firefox benutzen) bzw. die Lage der Ellipse an der Hyperbel (download hier).